An advanced 2048 AI with a Python frontend and C++ backend. Inspired by the bot created by nneonneo, it uses expectimax decision trees, bitboards and bitwise matrix operations to efficiently calculate each move leading to optimised performance, winning 100% of trials thus far. The GUI and game running logic uses Python tkinter and was taken from this repository written by a user named andersqiu - I tinkered with this to integrate with the game logic in a seperate C++ file.

For those unfamiliar, 2048 is a simple game involving 16 tiles, where you have to merge tiles with the same number in order to get the highest score. When you move, all tiles shift in the direction you chose and tiles which are the same number merge and add together. A new new tile (a 2 or sometimes 4) also spawns in. As per the gif below (which admittedly moves a tad fast if you haven't seen the game before), how the game works is fairly obvious after watching it for some time - there are really no additional rules outside of what you see, just "get big tile".

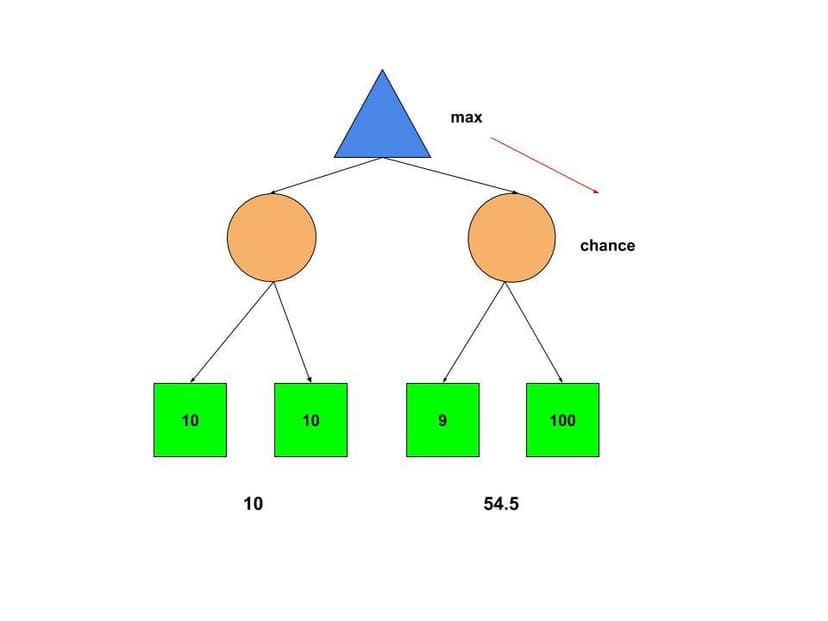
The bot finds moves using an Expectimax decision tree, which works similarly to the Minimax decision trees described here in a previous project . However, instead of every other layer being the prediction of an opponents best move, the opposing layer instead contains every possible outcome that could occur by chance, then taking the expected value of the score provided by each of those possible outcomes gives the score of the move. For more info on expectimax decision trees, this is a good resource. If you've read the details of my Checkers Bot project, the following diagram should make the small difference between the Minimax and Expectimax search algorithms fairly intuitive.

The main reason this performs so much better than the Checkers Bot, relative to other bots in their respective games, is largely thanks to the use of bitboards. To explain how this works, a brief revision of binary numbers is necessary. In our normal number system, which has a base of 10, each subsequent digit in the number represents a power of 10 - like below.

Most people are taught this in year 1 or so, and it becomes so intuitive you somewhat forget there can be an alternative way to write a number, but there is! In binary numbers, which are said to have a base of 2 instead of 10, each subsequent digit represents a power of 2 rather than 10. So the rightmost digit is the amount of ones (2⁰), then twos (2¹), then fours (2²), then eights (2³), and so on. When you see in pop culture computers using 1's and 0's, this is an example of what they actually refer to. See the diagram below for an intuition of how binary and decimal numbers represent the same numbers differently.

Back to the bot, what bitboards do is they cleverly represent the board with some binary number - how that is achieved or represented beyond that is arbitrary. So ideally, we want to find a way to represent the 2048 board with a binary number. Rough. Well first, we have to figure out how to represent a single square, then hopefully the board should just follow from that. We could just represent the number in the square with a binary number - a pretty easy solution. So if we allocated 8 bits (binary digits) to each square, we could represent 2 with 00000001, 4 with 00000010, 16 with 00001000 and so on. That's nice, but we're wasting a lot of space with all those zeros.

The reason we have all these extra zeros and only end up having a single 1 per square is because every number is a power of 2. Well hang on, if every number is a power of 2, what we can instead do is represent each square by the power of 2 of the number in it. Then we would represent 2 by 00000001, 4 by 00000010, 8 by 00000011 and so on. We can reach some pretty big numbers easily with this representation (representing powers makes it, by definition, exponential!), so to compress our board even more what we can do is shorten each square to 4 bits (and that still enables us to reach 1111 = 15, so 2^15. If we reach the 32000 square that's pretty solid)

Now each square can be represented by 4 bits, so with 16 squares, the entire board is contained in a 64 bit number. The reason we want to represent it with such a small amount of data is that the computer will simply process more information faster if our representation is smaller. This ends up meaning we can make our search tree far deeper due to how fast it is.

The bot includes many more optimisations on top of this useful data representation, the other main one being caching (storing previously calculated results) with the use of Operation Tables (storing the result of a move on every possible board, such that no calculations are needed) and Scoring Tables (storing the calculated score of every possible board board) which are explained in the README.md of the repository. That file will also explain to you how to run the bot on your computer, if you know how to use Github. Further optimisations are summarised well by nneonneo in this Stack Overflow post.

Even the reply on that post, however, doesn't grant as much of an appreciation for how optimised this algorithm is until you visit this file. If you know C++, the transpose_board function is a simple matrix transposition algorithm, but easily one of the most confusing but mind-blowing algorithms you'll encounter.